Standar deviasi atau simpangan baku adalah sebuah istilah yang dikenal dalam statistika dan probabilitas. Ini adalah ukuran untuk melihat sebaran statistik secara lazim. Rumus standar deviasi biasa digunakan untuk mencari nilai-nilai data yang tersebar. Rumus ini dapat pula mencari rata-rata jarak penyimpangan pada data yang didapatkan tersebut.
Mengenal Standar Deviasi
Istilah standar deviasi atau simpangan baku mulai diperkenalkan oleh Karl Pearson pada 1894. Ia menuliskannya pertama kali dalam buku berjudul On the Dissection of Asymmetrical Frequency Curves. Dalam Statistik, wilayah data yang ada di antara +/-1 memiliki simpangan baku sekitar 68.2%. Wilayah data yang ada di antara +/-2 memiliki simpangan baku sekitar 95.4%. Sementara itu, wilayah data yang ada di antara +/-3 memiliki simpangan baku sekitar 99.7%.
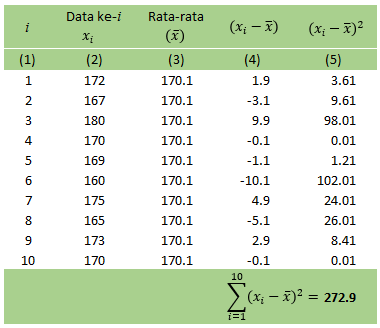
Simpangan baku adalah bilangan tak negatif. Satuannya sama dengan data yang digunakan. Jadi, jika diukur dalam satuan meter, simpangan baku atau standar deviasi juga didapatkan dalam satuan meter. Simpangan baku ini diartikan sebgai akar kuadrat varians.
Apabila nilai standar deviasi adalah 0, ini menandakan bahwa nilai dalam data tersebut semuanya sama. Namun, jika nilai standar deviasi semakin besar, ini berarti bahwa jarak titik data dengan nilai rata-rata akan semakin besar.
Rumus Standar Deviasi
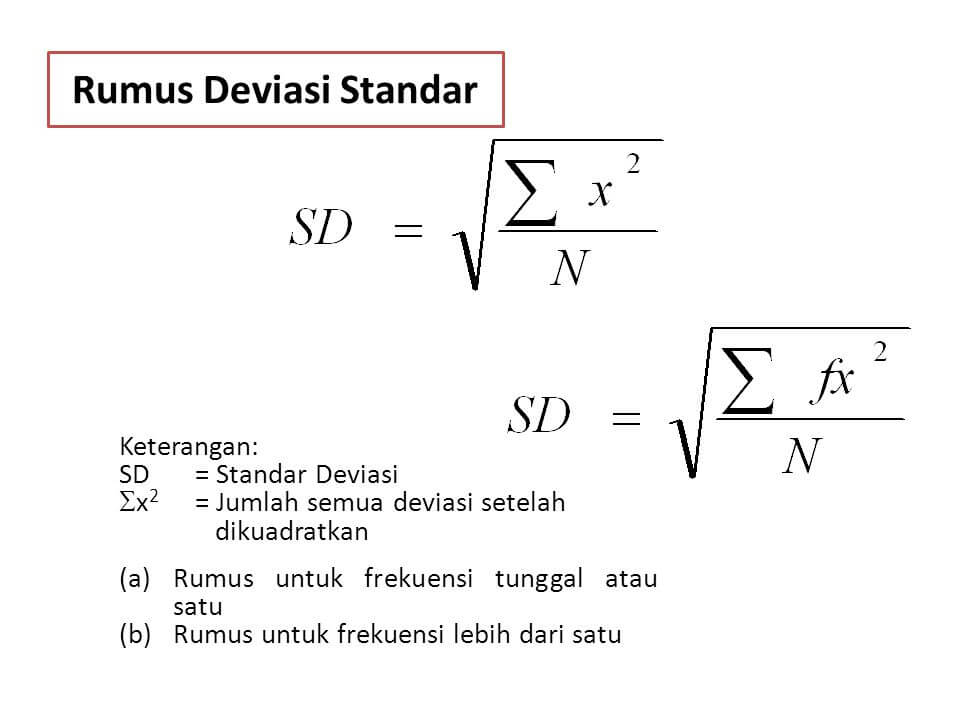
Simbol standar deviasi adalah huruf s. Untuk mencari nilai standar deviasi, hal pertama yang perlu diketahui adalah nilai rata-rata pada data tersebut. Ada empat rumus simpangan baku yang digunakan untuk mendapatkan nilai standar deviasi.
Pertama, rumus standar deviasi data tunggal. Rumus tersebut dapat dijabarkan sebagai berikut:
Kedua, rumus standar deviasi data populasi. Rumus tersebut dapat dijabarkan sebagai berikut:
Ketiga, rumus standar deviasi data kelompok untuk sampel. Rumus tersebut dapat dijabarkan sebagai berikut:
Keempat, rumus standar deviasi data kelompok untuk populasi. Rumus tersebut dapat dijabarkan sebagai berikut:
N adalah ukuran banyaknya data yang diambil. Fi adalah frekuensi. σ2 adalah varian untuk populasi. S2 adalah varian untuk sampel. Xi adalah titik tengah.
Nah, untuk menghitung standar deviasi, ada beberapa cara yang bisa dilakukan, yaitu:
-
Menghitung standar deviasi data tunggal
Langkah pertama menghitung standar deviasi data tunggal adalah mencari dahulu nilai rata-ratanya, kemudian carilah standar deviasi tunggal.
-
Menghitung standar deviasi data populasi
Langkah pertama yang harus dilakukan sama dengan sebelumnya yaitu mencari dulu nilai rata-ratanya, kemudian cari standar deviasi populasi.
-
Menghitung standar deviasi dengan excel
Masukkan data dalam tabel excel. Kemudian, gunakan formulasi berikut.
Untuk data sampel: “=STDEV(number1;[number2];….[number4])”
Untuk data populasi: “=STDEVP(number1;[number2];….[number4])”.
Manfaat Standar Deviasi
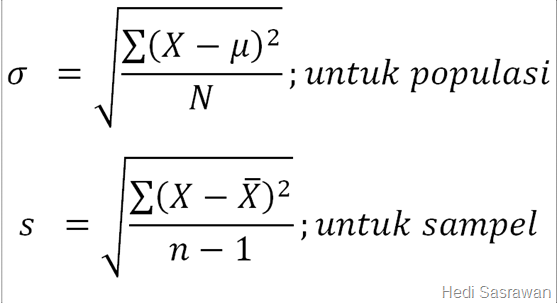
Dalam ilmu statistika, perhitungan standar deviasi dilakukan untuk mengetahui apaka sampel data yang diambil tersebut telah cukup mewakili seluruh populasi yang ingin didata. Perlu disadari bahwa sangat sulit atau hampir tidak mungkin untuk mencari data yang benar-benar tepat dalam suatu populasi. Nah, penggunaan sampel data menjadi metode yang dianggap paling efektif dan benar.
Supaya lebih jelas, perhatikan contoh ini. Jika seseorang ingin mencari tahu berat badan orang dewasa perempuan di dalam suatu negara, sangat tidak mungkin untuk menanyakan hal itu kepada satu demi satu orang dewasa perempuan. Selain sulit, tentu dibutuhkan waktu yang sangat lama serta biaya yang sangat besar.
Dengan statistika, peneliti hanya perlu mengetahui berat badan beberapa orang dan menghitung rata-rata serta standar deviasi. Dari data tersebut akan dapat ditemukan data berat badan yang paling mewakili seluruh populasi orang dewasa perempuan. Jadi, ilmu ini sangat penting untuk dipelajari.