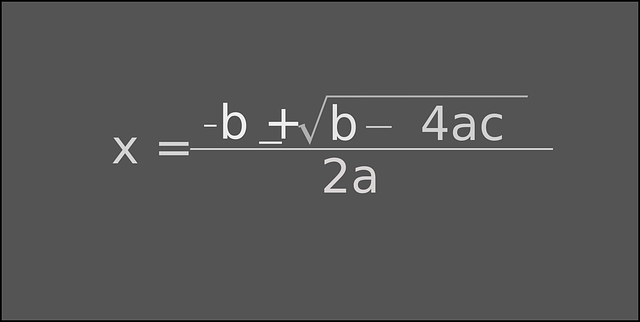Ada beberapa cara yang bisa digunakan untuk menyelesaikan persamaan kuadrat, yaitu pemfaktoran, melengkapi bentuk rumus ABC, dan menggunakan rumus kuadrat. Metode yang paling sering digunakan adalah menggunakan rumus kuadrat atau dikenal juga sebagai rumus ABC.
Apa itu rumus ABC? Rumus ABC adalah rumus untuk memecahkan soal persamaan kuadrat. Disebut rumus ABC karena di dalamnya terdapat formula a, b, dan c. Masing-masing merupakan koefisien x2, koefisien x, dan konstanta.
Meskipun tampak sederhana, rumus ini perlu digunakan dengan teliti terutama saat menulis dan mensubstitusi nilai koefisien dalam rumus tersebut. Inilah penyebab sering terjadinya kesalahan ketika menghitung akar persamaan kuadrat.
Ada beberapa syarat yang harus terpenuhi agar rumus ABC berlaku, yaitu:
- Persamaan kuadrat harus memiliki bentuk ax2 + bx + c = 0
- Nilai a ≠ 0
- Diskriminan (D), yaitu bilangan yang bersama dengan tanda akar sama dengan b2-4ac
- D>0
Ada pun formula yang bisa digunakan untuk memecahkan persamaan kuadrat umum adalah X1,1 = -b + b2 – 4ac √2a. Rumus ini dapat digunakan untuk mencari persamaan kuadrat yang menggunakan koefisien a<1, a=1, dan a>1. Diskriminan adalah D>0, D=0, dan D<0. Pada beberapa kasus, kesalahan sering terjadi karena tanda minus pada nilai b tidak disertakan.
Contoh Penyelesaian Soal dengan Rumus ABC
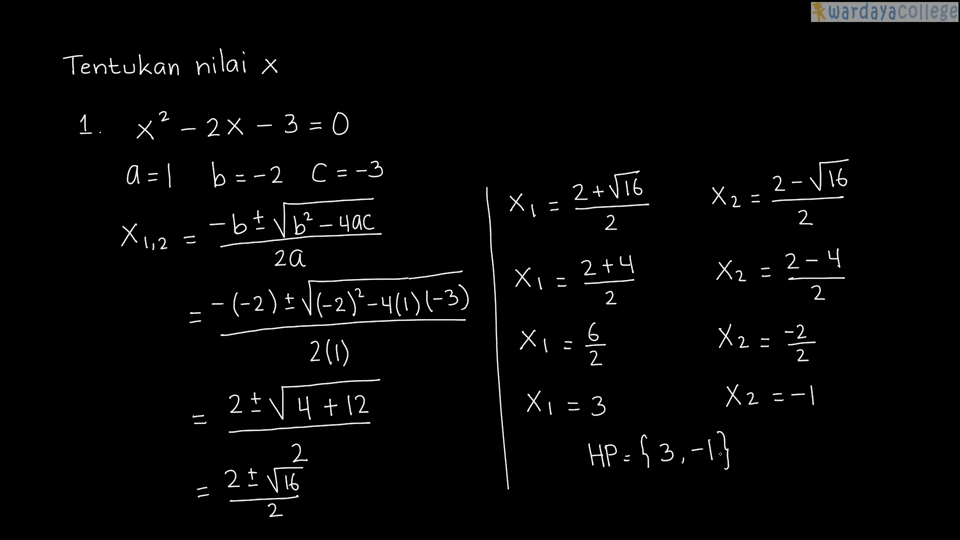
Nah, untuk memahami lebih lanjut tentang rumus ABC, berikut beberapa contoh soal dan penyelesaiannya.
-
Carilah akar persamaan kuadrat dari x2 + 7x + 10 = 0.
Sebelumnya, kamu perlu memetakan komponen pada soal tersebut, yaitu koefisien x2 yang disebut a, koefisien x yang disebut b, dan konstanta. Dalam hal ini, koefisien x2 atau a adalah 1, koefisien x atau b adalah 7, dan konstanta atau c adalah 10.
Selanjutnya, masukkan komponen tersebut pada rumus x1,1 = -b + b2 – 4ac √2a sehingga menjadi: x1,2 = -7 + 72 – 4x1x10 √2×1
Jadi, x1,2 =-7 + 49 – 40 √2
=-7 + 9 √2
x1 = -4/2 =-2
x2 = -16/2 = -8
Himpunan sama dengan (-2, -8)
-
Carilah akar persamaan kuadrat dari x2 + 3x – 10=0
Pada soal ini, a adalah 1, b adalah 3, dan c adalah -10
x1,2 = -b + b2 – 4ac √2a
= -3+ 32 – 4 x 1 x (-10) √2 x 1
= -3 + 49 √ 2 x 1
= -3 + 7
x1 = 2
x2 = -5
Himpunan sama dengan (2,15)
-
Carilah akar persamaan kuadrat untuk 2x2 + 4x – 6 = 0
Pada soal ini, a adalah 2, b adalah 4 dan c adalah -6
-
x1,2 = -b + b2 – 4ac √2a
x1,2 = -4 + 42 – 4 x 2 x (-6) √ 2 x 2
= -4 + 16 – (-48) √ 4
= -4 + 64 √ 4
= -1 + 2
X1 = -3
X2 = 1
Jadi himpunan sama dengan (-3, 1)
Nah, demikian beberapa contoh soal yang menggunakan rumus ABC pada pelajaran matematika. Hal yang perlu diperhatikan adalah angka yang menyertai tiap koefisien. Dengan menggunakan rumus ini, Anda akan lebih mudah mencari jawaban atas soal-soal yang diberikan. Nah, selamat mencoba!